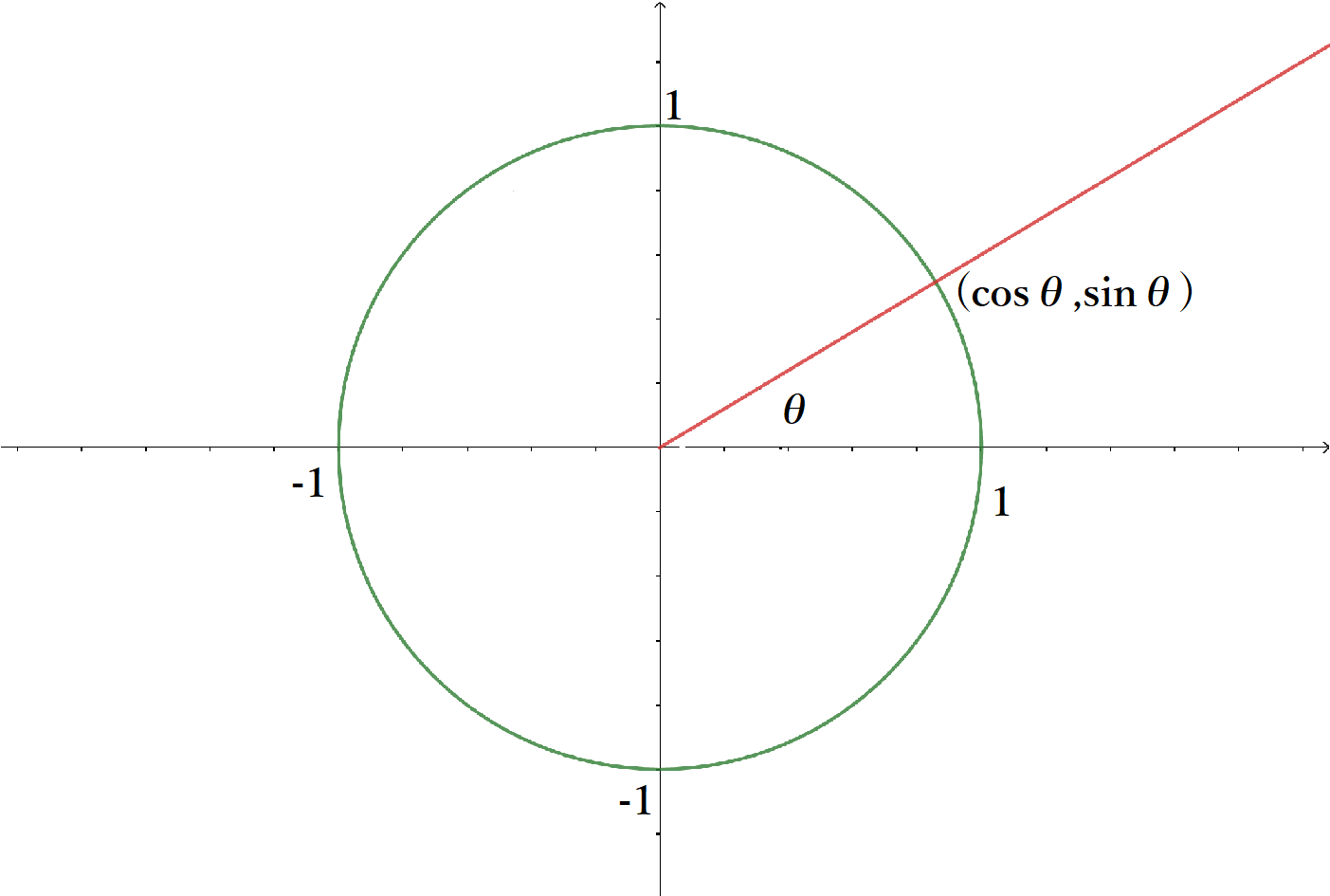
次に物理ではかなりの頻度で使われることになる三角関数について説明しよう。始めに三角関数の定義を示す。単位円と呼ばれる半径1の円をxy座標の原点を中心として設定する。x軸正の向きを基準として原点Oから半直線を作る。ここから反時計回りに $\theta$ 回転させたときの半直線と円の交点を$(\cos \theta, \sin \theta)$とする。そして、$\dfrac{\sin \theta}{\cos \theta}=\tan \theta$とする。

複雑な定義に見えてとっつきにくいので、三角関数のルーツから話をしていこう。そもそもは直角三角形の辺の比の話であった。三角形の相似条件を思い出そう。その1つは2角が定まることであった。直角三角形の場合には、1つの角は直角と定まっているので、残りの1つの角が定まればその直角三角形の形状が決定される。すなわち辺の比が角度1つで決まる。ここで、斜辺に対する高さや底辺の比を考えよう。
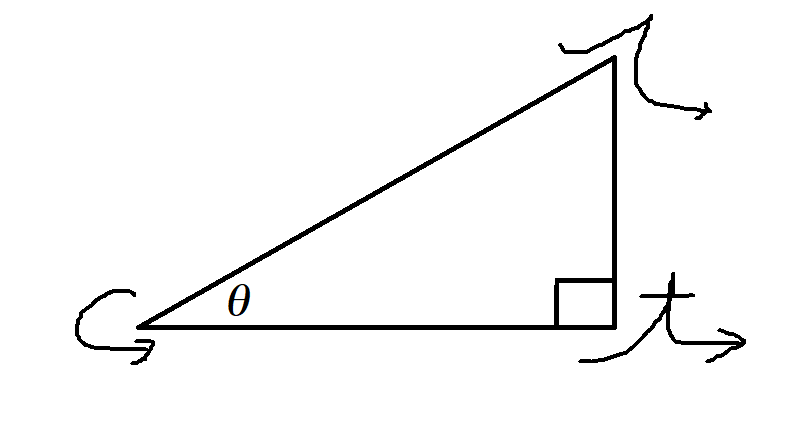
図のように $\theta$ を取り、このときの斜辺に対する底辺の比を $\cos \theta$ あるいは余弦、高さの比を $\sin \theta$ または正弦と呼び、底辺に対する高さの比を $\tan \theta$ 、 正接と呼ぶ。この定義は視覚的にわかりやすい。しかし三角形を作るためにも $0^\circ\lt \theta \lt 90^\circ$ でなければいけない。これをより広い角度に拡張しよう。
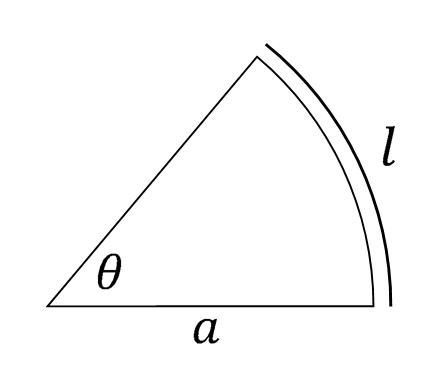
その前により数学的に使いやすい角度を導入しよう。まず、通常使われている「$^\circ$」を単位とするのは度数法と呼ばれる角度である。しかしこれは実数ではない。従ってこれを使った関数というのを考えることができない。そういう事情からも実数を用いて角度を定義したい。そこで全ての円が相似であることを用いる。相似であるので、角度 $\theta$ の扇形の弧長と半径の比は扇形の大きさによらず一定である。これでもしっかりと角度を定義することができ、実数でもある。このような角度の定義を弧度法と言う。例えば下の図の場合には、 $$ \theta = \frac{l}{a} \tag{1} $$ となる。
さて、三角関数の定義を弧度法を用いてより広い角へと拡張しようとしたのが始めに書いた定義である。
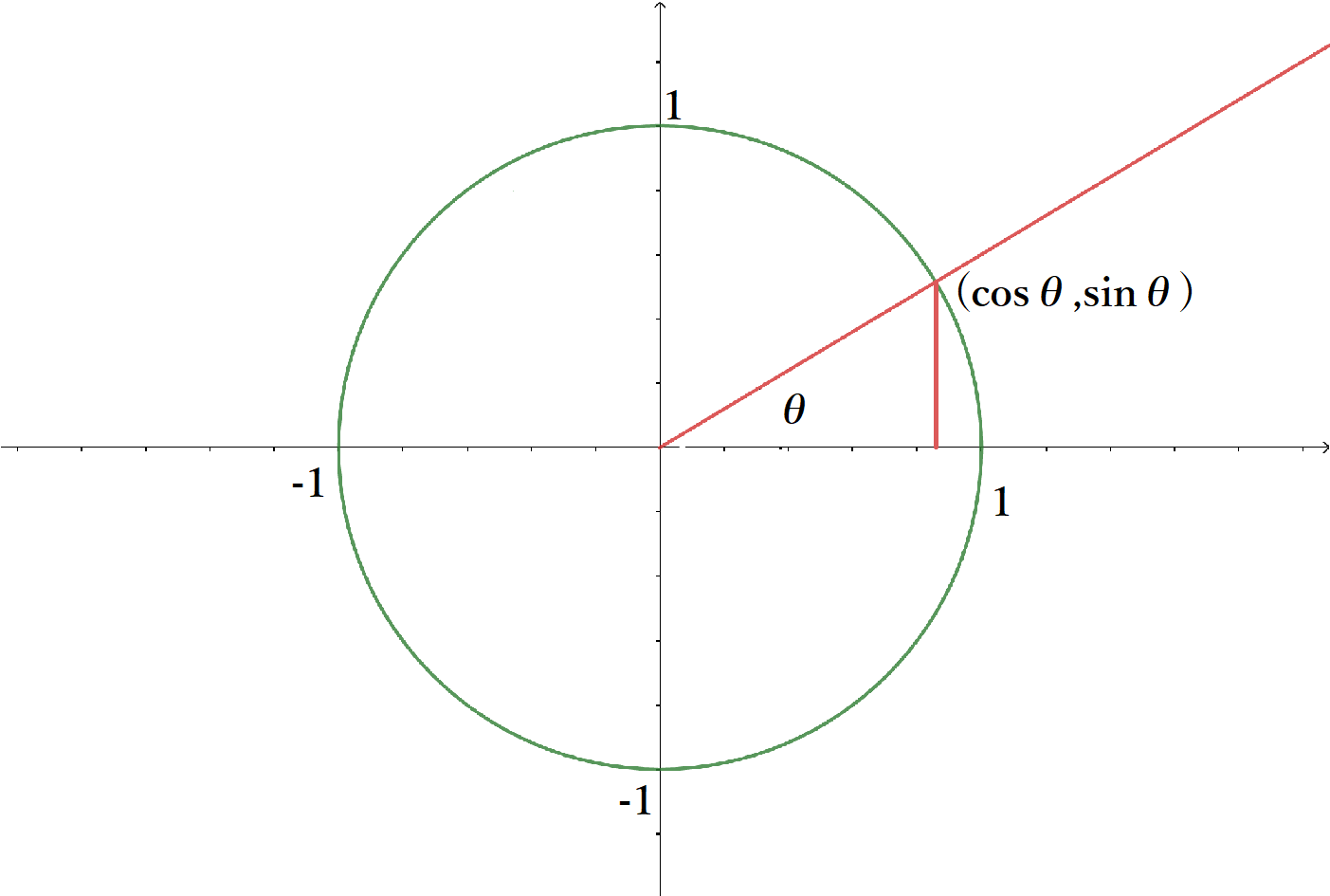
このように単位円を使った定義でもその中に直角三角形が出現し、角度も $0\lt\theta\lt\dfrac{\pi}{2}$ $(0^\circ\lt\theta\lt 90^\circ)$ に縛られない定義になる。
ここから三角関数の諸性質、定理を見ていこう。まず、単位円による定義から直ちに分かることがある。原点から $(\cos \theta,\sin \theta)$ までの距離はいくらだろうか。無論 1 である。従って次の関係が成り立つ。 $$ \cos^2 \theta+\sin^2 \theta=1 \tag{2} $$ 見慣れない表記だが、三角関数については$(\cos \theta)^2$や$(\sin \theta)^2$のことを$\sin^2\theta$、$\cos^2\theta$と書くことが多い。(2)の両辺を $\cos^2\theta$ で割ってやることで $$ 1+\tan^2\theta=\dfrac{1}{\cos^2\theta} \tag{3} $$ この関係も成り立つことがわかるだろう。これらの関係は非常によく使われるので覚えておこう。
次に、単位円による定義の見方を変えることで成り立つ関係を見ていこう。始めに、$\sin$ については単位円上のy座標を示しているのでその値はy軸に関して対称になることがわかるだろう。従って、時計回りを $\theta$ の負と取ったことに気をつけると、 $$ \sin(\pi-\theta)=\sin\theta \tag{4} $$ また、単位円はx軸に関してy座標の正負が変わるので、 $$ \sin(-\theta)=-\sin\theta \tag{5} $$
今度は余弦について考えよう。$\cos$ は単位円上のx座標を示しているので、その値はx軸に関して対称になるだろう。つまり、反時計回りでも時計回りでも同じだけ回転させれば同じ $\cos$ の値を持つというわけだ。数式で表すと、 $$ \cos(-\theta)=\cos\theta \tag{6} $$ 単位円はy軸に関してx座標の正負が変わるので、 $$ \cos(\pi-\theta)=-\cos\theta \tag{7} $$
ここまでは $\sin$ なら $\sin$ 、 $\cos$ なら $\cos$ の変換だった。ここからは $\cos$ と $\sin$ の間での変換を紹介しよう。図.1の図を"時計回りに $\dfrac{\pi}{2}$"だけ回転させよう。すると座標の見た目はほとんど変わらない。変わった部分はx軸とy軸の位置関係が入れ替わり、x軸の正の向きが回転させる前のy軸と真反対を向いている。この状態で半直線をy軸正の向きから $\theta$ 回転させよう。そしてこの状態のままで $\cos\theta$ の値を考えてみよう。軸を回転させた状態では $\cos\theta$ の値はy軸の値に対応する。では元の回転させる前の座標で見たらどのような状態になっているだろうか。始めに$\dfrac{\pi}{2}$だけ時計回りに回転させた。半直線はそのうえで更に $\theta$ だけ回転している。定義から単位円上のy座標の値は $\sin$ だった。従って、 $$ \sin\left(\theta+\dfrac{\pi}{2}\right)=\cos\theta \tag{8} $$ が成り立つ。同様のことを $\sin$ でも考えると、 $$ \cos\left(\theta+\dfrac{\pi}{2}\right)=-\sin\theta \tag{9} $$ も成り立つ。
正弦定理は任意の三角形とその外接円について成り立つ定理である。外接円とは三角形の頂点を全て通る円のことである。定理の主題は、外接円の半径を $R$ 、三角形の各辺を$a,b,c$とすると、
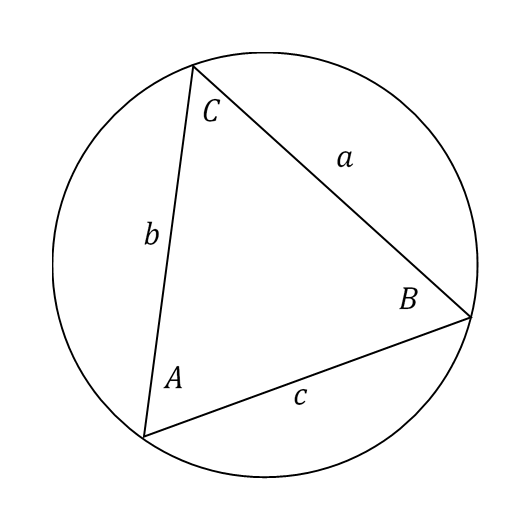
このような関係が成り立つ。この証明は円周角の定理を用いれば簡単に証明できる。
証明
正弦定理があるなら余弦定理もある。この定理は三平方の定理を拡張したものと考えるとすんなりと理解ができると思われる。
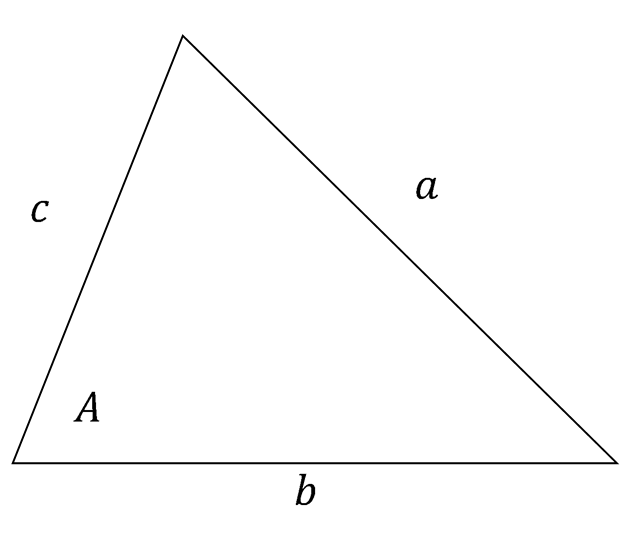
上図のような三角形について次が成り立つ。 $$ a^2=b^2+c^2-2bc\cos A \tag{11} $$ 証明
三角関数の値はよく知られた特定の角度でしか直接厳密に求めることが出来ない。そこでこの加法定理を用いると知った角度を用いて新たな角度のときの三角関数の値を求めることができる。便利な定理でとても良く使われるので証明していこう。
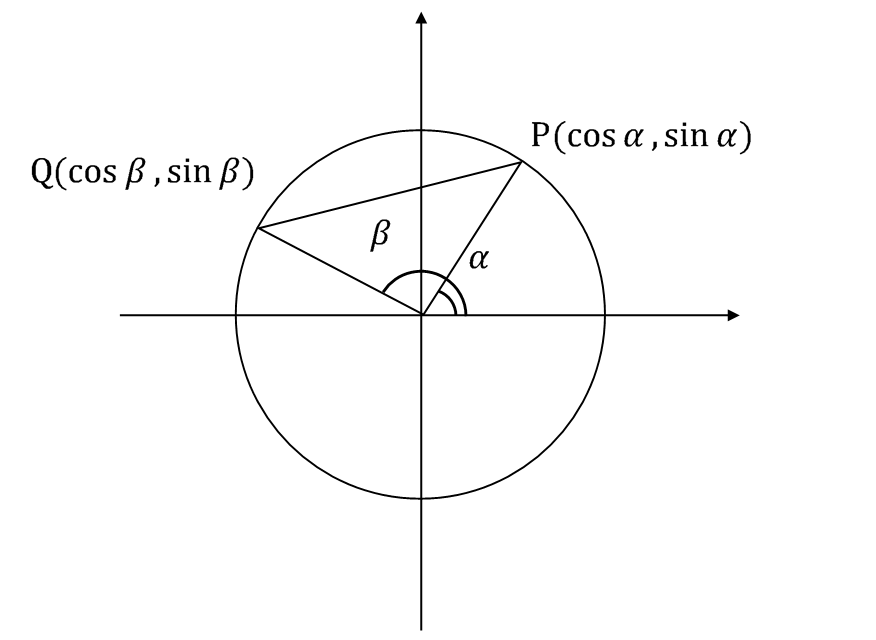
証明は$PQ$の長さを2通りの方法で求めることで定理を示す。まず、三平方の定理を用いて、 $$ PQ^2=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2 \tag{12} $$ 続いて、先程の余弦定理を用いて$PQ$を表す。ここで図.7の三角形の$PQ$以外の辺はともに長さ1であることに注意すると、 $$ PQ^2=1^2+1^2-2\cdot 1\cdot 1\cos(\beta-\alpha) \tag{13} $$ (12),(13)は同じものを指しているので、 \begin{align} (\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2 \\ =1^2+1^2-2\cdot 1\cdot 1\cos(\beta-\alpha) \\ \cos^2\alpha-2\cos\alpha\cos\beta+\cos^2\beta+\sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta \\ =2-2\cos(\beta-\alpha) \end{align} ここで(2)を用いて両辺を整理すると、 $$ \cos(\beta-\alpha)=\cos\beta\cos\alpha+\sin\beta\sin\alpha \tag{14} $$ と示すことが出来た。
ここで(14)の $\alpha$ に$-\alpha$ を代入して、(5)、(6)を用いると、 $$ \cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta \tag{15} $$ 続いて(8)、(9)について、少し変形をすることで \begin{align} \sin\left(\frac{\pi}{2}-\theta\right)=\cos\theta \\ \cos\left(\frac{\pi}{2}-\theta\right)=\sin\theta \end{align} となる。(14)の $\beta$ を$\left(\dfrac{\pi}{2}-\beta\right)$に変えて代入すると、 \begin{align} \cos\left(\frac{\pi}{2}-\beta-\alpha\right)&=\sin(\alpha+\beta)\\ \cos\left(\frac{\pi}{2}-\beta\right)\cos\alpha+\sin\left(\frac{\pi}{2}-\beta\right)\sin&\alpha=\sin\beta\cos\alpha+\cos\beta\sin\alpha \end{align} これらから$\sin$の加法定理も求めることができて、 \begin{align} \sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \tag{16} \\ \sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta \tag{17} \end{align}
$\tan$ に関しては定義から、 \begin{align} \tan(\alpha+\beta)&=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)} \\ &=\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\\ \end{align} 分子分母を $\cos\alpha\cos\beta$ で割ってやると、 \begin{align} \tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \tag{18} \end{align}
以上が三角関数の概要である。具体的な活躍のポイントは力学の項目で早い段階から出てくるはずである。